Thinking Notation #6
Fun Natural Language Inspirations
For spiffing up the notation. Sometimes the languages from farthest back reveal the most about the limits of human language. Sometimes the languages from the farthest back are the most mind-blowing and alien.
Spiffying Up the Notation
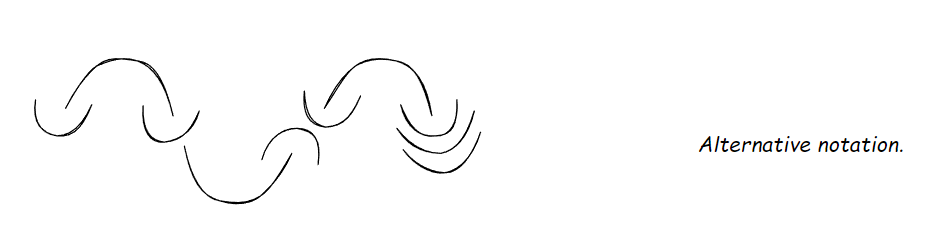

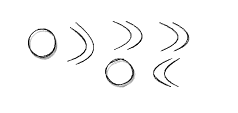
Check out optional syntax in Connection Theory.
Some Fun Subfragments
A simple tableux subfragment:
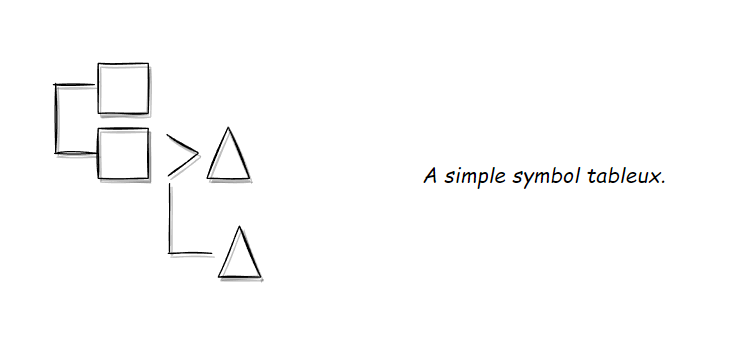
Regarding Substitution
Regarding a comment near the end of Thinking Notation #5.
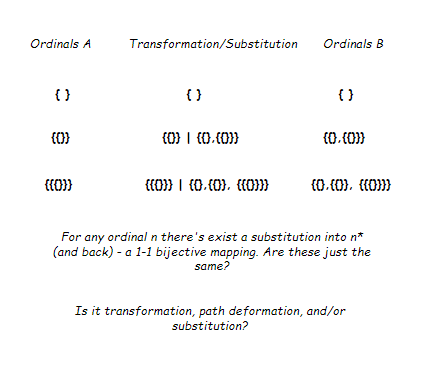
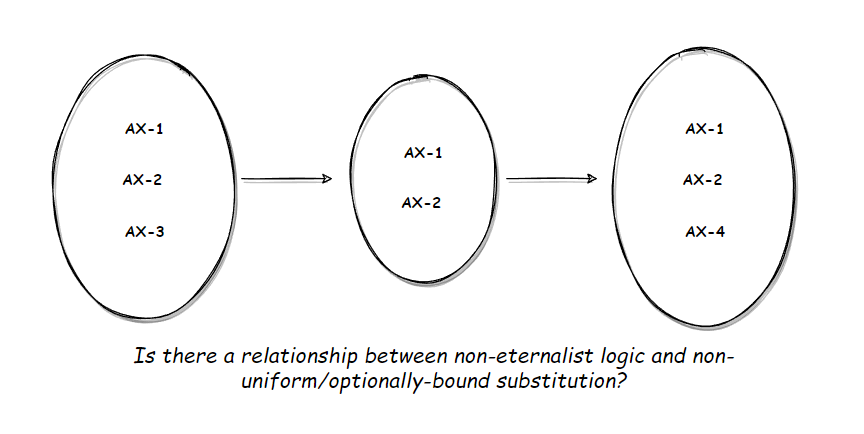
Regarding Non-Eternalist Logic
Is optional binding related to Non-Eternalist Logic and in what ways? (I think such operations can be modeled fairly cleanly as Non-Eternalist Logic.) Non-Eternalist Logic appears to be closely related and might be modeled under optional substitution (across axioms ... at least in certain cases).
Some Oddities
What are the precise demarcations between "valid" subfragments and "invalid" so-called False Langauges?

What’s interesting is that the relevant features of the language seem to be well-defined sub-fragments. It has many subfragments that seem completely esoteric and ill-defined. Some "regions" (to use a landscape metaphor) are populated with well-defined mathematical entities/systems (very familiar to us from the 20th century). Many wider "regions" seem completely anarchic. What's going on there? (I also don’t know of any other Formal Languages that have that property.)
Consider, First-Order Logic (the basis for computer languages like Prolog). One begins with a Lexicon (alternatively, an Alphabet or Vocabulary - some authors use that verbiage instead historically) with grammatical rules that recursively select from that background set of anarchic symbols a set of Well-Formed Formulae (wff). An attendant Proof System, Interpretation, and Structure (Truth-Assignment, Semantics) then combine to form a Logic. Not all Logics are useful to mathematical discourse and activity. A Logic must have certain properties: Soundness, Completeness, Closure, Deduction Thereom, etc. to be useful. (All that is just basic upper undergraduate and graduate coursework.) One might start with the same set of symbols (Lexicon) and then define wff for two or more languages.
But note the differences:
- Thinking Notation is Semantically Closed. The axiom system is the top-level Vocabulary and Proof System. By arranging two or more sequences together (allowed by the axioms themselves) we arrive a Semantics. There's no distinction between the traditional three pieces that are combined into a Formal System.
- In the FOL example above, the languages that are being constructed are implicitly constructed within some higher-level Metalanguage that's never really defined (presumably it's a Natural Language such as English).
- Note also that the varying appropriateness of Logics that share a common Lexicon mostly comes down to their Proof Theoretic properties (which, under the current conception of a Logic, reside not in the Language but in the Proof System).
So, it seems to be a fairly distinct and even novel phenomenon unique to (systems like) Thinking Notation.
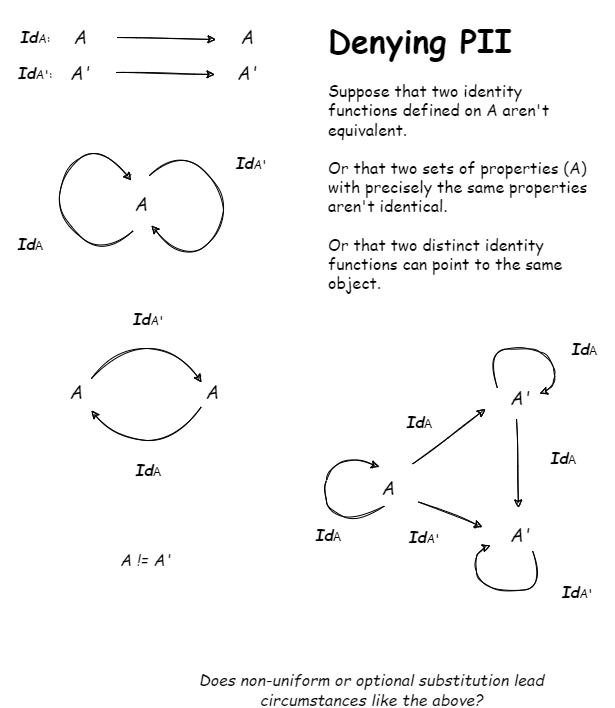
Regarding PII
If we deny the Principle of the Identity of Indiscernibles what are we left with in our systems? (This has been discussed in the context of Quantum Particles which seem to violate PII.) Is there a relationship between the denial of PII and optional binding/substitution?
Here's a fun, simple, wild, scenario:
Regarding Relational Notions

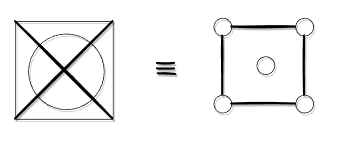
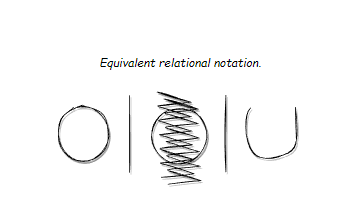
The above depicts Sign, Identity, Relations.
- Thinking Notation
- Thinking Notation #2
- Thinking Notation #3
- Thinking Notation #4
- Thinking Notation #5
- Thinking Notation #6
post: 12/12/2022
update: 12/16/2022