Thinking Notation
I was inspired to work on the kind of general thinking system aimed at by Leibniz (characteristica universalis) and Frege (Begriffsschrift).
Thinking systems of this kind typically fall into at least one of the following three motivational categories (and most of the grand logic programs of the 20th century aimed for all three):
- Descriptive - to describe a function of thought as it is performed and observed being performed by denizens of the world.
- Normative - to define what proper, correct, ideal, or obligatory kinds of thinking are.
- Justificatory - to prove, have the ability to justify through proof, or to define a system of inference rules.
The aim here is Descriptive and not say Justificatory - e.g. the basic axiom schemata here describe a pattern of thinking that does need necessarily track truth but rather describes the ways that thoughts, true or false, follow sequentially (rather than as a result of logical consequence).
Simple Outline (2012)
I will depict through several axioms a few kinds of thinking (techniques) that when combined with other formal systems, imbue them with richer power:
- I will use a few simple diagrammatic objects (in a way amenable to axiomatic approaches):
i. @, >, ^ - these symbols represent an item of thought (which is quite approximate but will suffice).
ii. | - denotes a temporal transition in thinking.
iii. Thus, > | > represents the same item of thought over a single transition.
The same symbol on both sides of the | specify the same item of thought.
iv. Other marks will be introduced as well, specific to the exact operation axiomatized.
- These diagrammatic objects can be concatenated (combined) to form streams of thinking.
Axioms
- Identity - to hold the same thing in mind across transformation: > | >
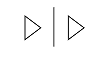
- Specificity - to clarify and expand a thing in the mind: > | @ - ^
i. "The house on the street" - "the dining room is next to the front entrance in that house on the street".
ii. Here the - represents a relational symbol.
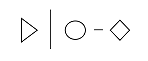
- Abstraction - to blur or obfuscate the details of something: @ - ^ | >
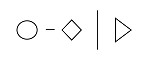
- Separation - to isolate or compartmentalize two items: @ - ^ | @ ^
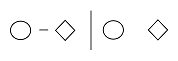
- Replacement - to replace one symbol for another via substitution: > | @
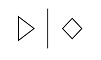
- Elimination - to eliminate a symbol of thought from the present stream of thinking: > @ | >

- Existence - to introduce a symbol of thought into the present stream of thinking: > | > @

Comments
i. Every stream starts with a single symbol of thought: >.
ii. Each of the axioms above have a dual opposite (except for Identity and Replacement).
iii. Thinking proceeds through distinction (difference) or symmetry breaking (as described in Spencer-Brown's Laws of Form).
Read: Additional Comments
- Thinking Notation
- Thinking Notation #2
- Thinking Notation #3
- Thinking Notation #4
- Thinking Notation #5
- Thinking Notation #6
post: 4/15/2012
update: 11/18/2018
update: 4/2/2020