Thinking Notation #3

Read: previous entry

Semantics

Semantics for Thinking Notation can be constructed from two syntactically valid Thinking Notion streams of thought (or, thinking sequences).

Recovering Boolean Algebra

Deriving the semantics for Boolean Algebra from Thinking Notions is a straightforward affair. We can compare two thinking sequences (henceforth, sequences) and evaluate them as True or False if they are identical or not.

Recovering Predicate Calculus

Using the Grouping syntax specified previously, we can also construct the necessary resources for the semantics of Predicate Calculus.

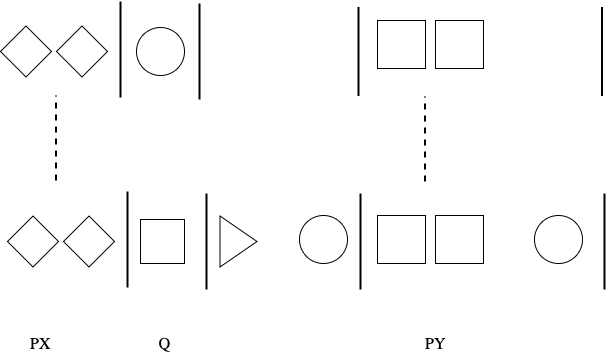
We can also substitute the traditional First Order syntax as needed (by associating constants, variables, and quantifiers with items in a thinking sequence).

Semantics of Semantics

Sequences of sequences can also be formed.

This can be used to represent familiar model-theoretic model classes or sets of interpretations.

As a Higher-Dimensional Logic

Naturally, sequences of sequences can be used to construct dimensional and higher-dimensional logics.