Thinking Notation #2
Building off the simple idea from before or following notes.
Below, I will discuss a few, fragmentary, ideas that expand the original conception and imbue it with greater expressive power.
Extension: Types or Categories
- Type - specifies a category or typing shared between two items of thought: @ > | @> both > and @ belong to the same category and are placed adjacently.
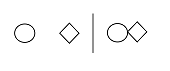
- Grouping - gives a handle, monniker, or label to a category: @> | ^ - ^ is the name for the category to which > and @ belong.
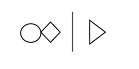
Practically, this allows Thinking Notation to acquire predicate-like expressive power. I am unaware of an any other existing alternatives (in the foundations of logic and maths) to Set Theory, Type Theory (which is typically introduced via some background Set Theory), or Predicate Calculus that allow a formal language to accomplish that.
Extension: Sublation
Where two diametrically opposed items are demonstrated to be:
i. A pseudo-conflict - the two items are semantically meaningless (vacuous) or irrelevant.
ii. Demonstrated to be the same item upon further examination.
iii. Are discarded in favor of third item that bears some features of both previous items.
Read: Hegel and Logical Modules.
Derived Rules
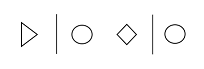
- Focus - Focus on one item: > | @ > | @ (Note: that the image below depicts this axiom after the suppressed application of the Replacement axiom.)
Extension: No Limit
The | symbol does not specify a contiguous item of thought nor an immediately preceding one. Rather, it can be any preceding item of thought (symbols are bound across transformation regardless).
Here, the axiom rules (which were previously purely mechanical and sequential) become axiom schema with universal substitution.
- Thinking Notation
- Thinking Notation #2
- Thinking Notation #3
- Thinking Notation #4
- Thinking Notation #5
- Thinking Notation #6
post: 12/14/2018
update: 12/24/2018
update: 4/2/2020