Remarks on Truth-Grounding and the Liar #2

Summarizing, linking, and uniting several topics.

For the DRAFT Constraint Satisfaction and Classical Extensions of KF.

Algorithm Implementation

GitHub

Additional Tarskian Considerations

Tarski 1944 defines each Meta Language Mₐ as containing a target Object Language Oₐ such that a Truth Predicate for a (Tₐ) is present in Mₐ about WFF in Oₐ (but not present in Oₐ).

Tarski's approach appears to commit one to the following:

1. An infinite ascending hierarchy of languages.
2. Profligate Truth Predicate Pluralism - an infinite ascending hierarchy of Truth-Predicates. Each Truth-Predicate is immanent in each linguistic ascent.
3. In the absence of Bridge Laws or other subsumption laws, each ascending Truth-Predicate will express more Truths at each ascent than those below it (where n = a + 1, Tₙ doesn't exist in Mₐ and so WFF with Tₙ don't exist at all below n). So, each Truth Predicate fails to express the totality of truths (e.g. - all > a) at each level a. It's a Partial Truth Definition at each level.
4. Since it ascends infinitely, there's no top-level Truth Predicate capable of expressing all Truths.
5. While at each level a, the Liar Sentence is blocked for a, it can be recovered at > a for a. And since each WFF (including T-Scheme at level a) is contained in each ascent, the Liar Sentence re-emerges for < n at n.

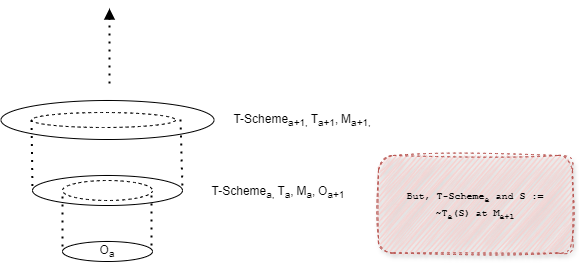
How then are we justified in taking T-Scheme through such an approach:

1. As a correct, universally quantified expression, schema, or law (even within the Object- and Meta Langauge hierarchy since we cannot find a top-level Truth Predicate)?
2. How do we identify which Truth-Predicate we're to use given that each Truth-Predicate is Partial and there are at least n-many such predicates for each ascent n?
3. And why not move to n+1 since the ascent n is contained in n+1? (Why one ascent level over another?)