Symbol Binding

I've talked about traditional cultural tropes and folklore that have found their way into the modern world: Techne and Philosophy - "it is the same at the end as it is at the beginning" perhaps rings more true now than ever. Examples:

1. Golems and Robots
2. Runes and CPU Fabrication Techniques
3. Spells and Algorithms
4. Fortune Telling and Future Forecasting
5. Scrying and Computer Monitors

Semantic Immuration and the Binding of Symbols

One intriguing notion I've alluded to regards the ability to permanently affix the meaning of an Expression (by wrapping the Language the Expression is part of within the Expression itself). An Expression exhibiting Semantic Immuration is bound in a sense since the meaning is singular, one, and univocal. The Language is only partially public since it is "visible" but cannot be "deformed" (is not subject to semantic drift).

Continuing with the notion that modern technology and mathematical techniques are often incarnations of ancient folk notions under new branding we might think of "binding" an Expression in such a way. For example, let the symbol ⊡ (I've randomly selected Unicode symbol 22A1) stand for the application of that Function (of wrapping the Language of the Expression within the Expression itself).

For convenience let's also suppose we preclude any fixed-points or the like (stipulated as part of the meaning and definition of the binding symbol ⊡).

Then, the Expression Q for some Expression Q := ⊡P specifies:

1. The indefinite fixed semantic integrity of P as Expressed by Q. Any shift in interpretation, meaning, etc. w.r.t. to P as set by Q is simply a different Expression R such that R ≠ Q.
2. Suppose we define the binding symbol (⊡) such that its being applied twice returns the Expression to its original prebound state. Then, ⊡Q := P which uniquely specifies P as expressed by Q.
3. We might also define the binding symbol in such a way that iterative concatenation does return the original Expression but rather "strengthens" the binding already in place.
4. In both cases, we can define the very rules of the binding symbol in such a way that any comprising axioms are immutably fixed forever. Thereby, permanently fixing the meaning of the binding as Expressed by those rules.

This reminds me both of the kinds of immutable deontic commands that are found across various religions equally as well as it does the kinds of "Devil's bargins" often found in folklore. If (some) kinds of Language vary or alter, there are clearly cases where it might be useful or desirable for Language to remain fixed eternally.

Chiastic Expressions

Going from the other direction, can we construct Expressions that always change in their meaning? Yes, we can do so in a similar fashion.

1. Consider the following symbol ⊛ (I've randomly selected Unicode 229B: https://symbl.cc/en/229B/).
2. Suppose that unlike the prior, binding symbol, we make ⊛ stand for the operation the next time you read this Expression, the character *n* contained within this Expression, increments by 1 since the last time you did. If it's the first time you've read the Expression then the value of *n* is 0.
3. So, P := ⊛(There are n apples I like eating.).
4. The first time one reads P it resolves to the semantic content: There are 0 apples I like eating.
5. However, on a second reading, the content has changed: There are 1 apples I like eating.

These are akin to Chiastic language (or pictorial) chains as found throughout the writing systems of Classical Antiquity. Here, the symbol "carries" and "stores" information (as it were) not contained within the Expression itself.

These are obviously very simple examples and we can conjure up many more that are a bit more complicated farily easily. I think these kinds of Expressions lend themselves nicely to Non-Eternalist Logic and represent an extreme from which binding (above) is designed to prevent or delimit.

Lambda Expressions

The most obvious and natural go-to for how Symbols are bound conventionally is the Lambda Calculus. Lambda Calculus-esque Symbol Binding is basically assumed in almost every existing formal mathematical system (that I'm aware of at least).

I've discussed how we might "take the other route" here wherein one allows for Uniform Substitution to fail (Optionally-Bound Substitution).

Let's discuss this notion a bit more:

After originally posting this, I found a great and related research talk from the awesome folks at Microsoft Research and the Carnegie Mellon Department of Philosophy. Dr. Roux gives an Abstraction example that demonstrates the move from concrete instances to a general abstract Lambda Calculus expression at 3:09 - he uses the symbolic notion: (λz.z + x + z + y + z)1 which is cool since it's superficially similar to the above and was discussing some related and converging topics.

1. When we see Letters (Symbol Tokens) we instinctually identify them as one in the same Letter (or as instantiations, etc. as such). When we replace Letter Tokens with geometric Shape Symbols the Symbolic associations become more pronounced.

i. This gives rise to the following kind of question: what truly establishes the equivalence of two occurrences of the same Shape in these Expressions? (Indeed, arguably, the Lambda Calculus is interesting because it helps to articulate these notions precisely.)

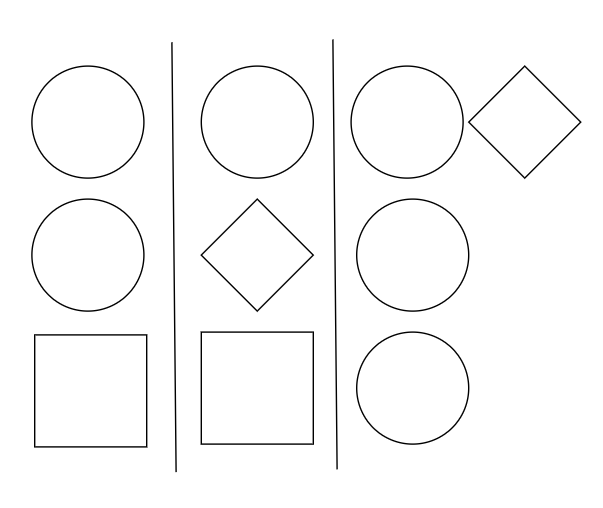
ii. Consider the first and the second occurrence of the geometric Shape Symbol ◇? (As stated, the human mind automatically associates and links the Letter Tokens but when we use other kinds of notation this implicit linkage falls away. The Cognitive Science behind that is intriguing but is a tad tangential to us presently.).

iii. Needless to say, Uniformly Bound Substitution operates on the level of those implicit Lexiographical Isomorphisms (sameness in Letter Token Shape).

iv. So, by denying mandatory Uniform Substitution for Symbols that are Bound, perhaps we move closer to unpacking and dislodging some of the implicit dogmas at work in the human mind that taint the purity of our Language and thinking systems.

2. Optionally Bound pertains to the ○ Symbol above not the □ Symbol.
3. Optional Binding is also not just equivalent to every Symbol being Free:

i. A Symbol (or Term) being Free can be Expressions themselves and that can contain Uniformly Bound Expressions.

ii. No wff will exist in a First Order Expression that has any Unbound, non-Constant, Free Variables (which are uniquely specified via stipulated definitions - typically, :=). As such, there are no Variables that either aren't Bound or that lack a precise mapping into the Domain (period) in any grammatically-valid First Order Logic Expression.

iii. It's important to stress that the concept of Free and Bound Variables apply at the level of the Expression whereas the concept of Optional Binding applies at the level of the Binding Operator.

iv. In the absence of Uniform Binding there's no other formal notion of Symbol Binding around. So, restricting all Variable Substitution to being Free apparently wouldn't allow for any Substitution at all.

4. The formal definition of Free Variables helps to provide a specific, precise, notion about when and how Variables are Bound (a notion essential to Logic and Mathematics). It also (indirectly) helps to specify how Symbols can in some sense "be the same".
5. In the systems I've sketched out there is still an association between two Symbols that look similar although the relationship is weakened.

i. Lexiographic Isomorphism does not necessarily entail the same treatment under a Subsitution Operation.

ii. The identification of Symbol Tokens by Lexiographic Isomorphism is not assumed.

An example of a sequence of Symbols replaced via Optional Subtitution: