Relational Bundles and Graphs

A few comments and clarificatory remarks about the distinctions between Graphs (as a mathematical concept and as a database design approach).

Graphs

A Graph (as studied by mathematicians) defines:

1. A Set of Vertices (Nodes)
2. A Set of Edges that hold or obtain between Vertices

Edges can be Directed or Undirected.

Note that Categories are not Graphs in the sense above. (See also: https://math.stackexchange.com/a/1239207 and https://mathoverflow.net/a/384839.)

Graph Databases

Graph databases are a kind of NoSQL (Non-Relational) database that's probably easiest to comprehend by contrasting against other common database patterns:

1. Document Databases - specifically refer to a kind of NoSQL database whereby data is stored in Collections of Documents with (potentially deeply) nested Embedded Documents and/or by "pointing" to other Documents (via DBRefs or DocumentReferences - note that DocumentReferences are essentially what are called No-Constraint (Weak) Foreign Key Associations).
2. Relational Databases - specifically refer to a kind of Relational Database which supports some Structured Query Language dialect whereby data is stored in Tables by Row and Column with associations between data points being specified by Foreign Key relationships (that are defined on Tables and which support JOIN operations).

Graph Databases, by contrast, query by a "set" of interconnected data points (inspired by the mathematical notion above). From the Meta official blogs and documentation:

• "Every data item, such as a user, check-in, or comment, is represented by a typed object containing a dictionary of named fields."
• "It represented data items as nodes (objects), and relationships between them as edges (associations).
• Typed Objects (Graph-Theoretic Vertices) are connected by explicit associations (Graph-Theoretic Edges) bidirectional, symmetric, etc.) to other such Typed Objects.

Despite those specific differences, I think Functional Programming and Graph Databases are most in the spirit of and aligned with the philosophical notions I've introduced.

Philosophical Objects

Some intuitions about Object-Hood that have been defended throughout philosophical history:

1. They have boundaries. (Think Encapsulation in Computer Science and Programming.)
2. They are (usually) spatial or at least located in some background space or universe. (Whether in Cyberspace, Heap Space, or Physical Space.)
3. They self-subsist (do not flicker in and out of existence - they persist, endure, perdure - one of the wonders about modern particles and Quantum Foam is that they defy this intuition).
4. When overlapping, they retain their individual essence or identity (they neither merge nor blend, they are merely arranged in some kind of spatial arrangement, e.g.).
5. They can be grouped or clustered together (to form or be contained within a Container which may itself be an Object as Sets are currently seen as).
6. They are the referents of singular terms - what names refer to.
7. They obey Leibniz's Principle of the Identity of Idiscenernibles (which Quantum Particles appear to defy).
8. They are discrete.

Relational Bundle

A Relational Bundle (what I've since dubbed a Connector) is a Non-Objectual Entity:

1. (RR) Legs may take relations.
2. (LL) Legs may take other legs.
3. (RS) Legs may take relational structures.
4. (BTR) Legs do not take anything other than relations, other legs, or relational structures.

(The original formulation.)

The choice of nomenclature is explained further here being inspired by the topological notion called a "pair of pants", key chains, and other trope-theoretic notions like compresence.

A slightly different formulation:

1. ◠ has one or many │
2. | take |
3. | take ◠

This can be compressed further (as I've demonstrated):

1. ▢ has one or many ▢
2. ▢ take ▢

Note that ▢, ◠, and │ needn't obey Uniform Substitution and/or Variable Binding (found in Lambda Calculus) - a key feature of the described approach is the denial of these common linguistic properties.

Take your pick from the variety of formulations thus far!

The perspective here is that connections, associations, and relationships are first-class citizens not secondary entities that link Objects (as an afterthought).

Note that Relational Bundle Diagrams so defined can express Graph Theory. Relational bundles are strictly more abstract or general than Graphs. I've even supplied a tentative alternative formulation of the Ordinals without recourse to Sets.

Purely Relational Databases

What might a "purely relational" database look like?

1. No Objects (Sets or otherwise) within its more fundamental ontological dependencies (let's just call those what they are.)

   • Which might form a model of Hyper Computation - e.g. - N+1 information units might be packed into N units inherently due the non-atomic nature of interwoven Relations.
   • The successor entities would lack certain intuitive features described above.
   • Note that every Computer Science paradigm today is objectual somewhere in its conceptual dependency tree.
   • Arguably, much more performant at handling deeply interconnected data (discrete or otherwise).

2. Something like light-wave propagation in Photonic Computing. (Exhibiting intrinsically connected wave-like behavior rather than discrete Objects bound by some kind of Relation.)

3. Consider something like the following path-based data structure.

   • Static Objects (or other entities) are "strung together" (query, associations) into a single relational entity (the depicted "golden braid"):

     

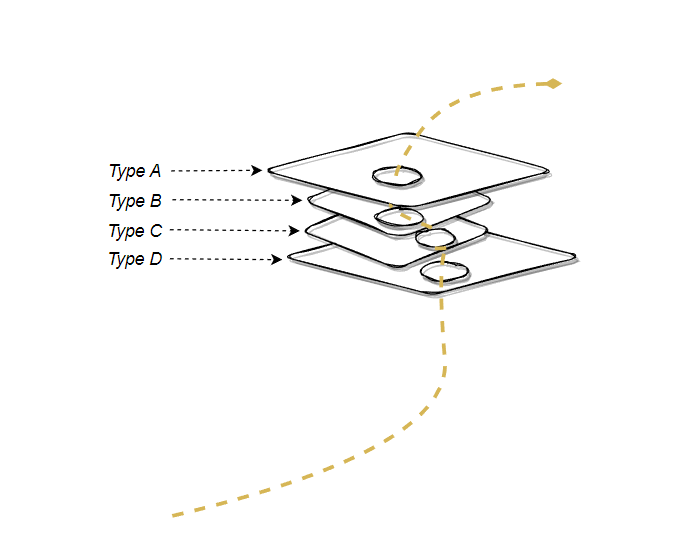
   • We observe that intutions surrounding data representation (Rows, Columns, etc.) can be seen as dual manifestations of the same:

     

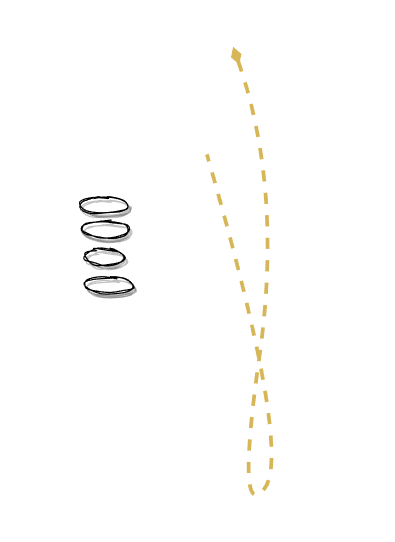
     And, that one of the two manifestations lends itself nicely to Relational Bundle Theory above.