Half Dimensions #2

I previously sketched the outline of an alternative to the reigning topological dogma that each spatial/temporal dimension is sharply bounded (to clarify, I'm not talking about fractal, Hausdorff, or self-similarity dimensions but rather representations of spacetime that allow for "partial" or non-integered quantities of dimensions):

1. That the number/numeric quantity of dimensions (and not the representation of a dimension using the Reals) is given by the Integers, Ordinals, and Natural Numbers.
2. That dimensions do not "overlap" in some sense. We position objects against all the dimensions in space but each dimension is independent and distinct. They do not "bleed into each other" so to speak.
3. Would such dimensions be "partial" dimensions? Or not sharply bounded (infinitesimal limits)? Both? What would that mean ontologically (what would be the human-friendly way of parsing that mathematical notion)?

Contra Descartes

All geometric and topological notions in modern use appear to rely on Cartesian multiples/products: e.g. - ordered n-tuples given by R ✕ … ✕ R.

Surprising to see Descartes' influence and legacy still holding sway over mathematics even in the 21st century!

So, accomplishing an alternative to the reigning dogma requires some alteration to the very foundations of geometric/topological thought. Going right up against titans in the history of philosophy and mathematics!

Specific Examples

Some specific examples:

1. A Euclidean space with 1.11 dimensions where each dimension is Natural Number-intervaled.
2. A pseudo-Euclidean space with 0.99999999... dimensions where each dimension is Real-intervaled.
3. A Riemannian manifold, Minkowski space with 3.14 dimensions where each dimension is Real-intervaled.
4. A Euclidean space with 2.5 dimensions where each dimension is Real-intervaled.
5. A Lorentzian Manifold with dimension r >= 2, r is not an Ordinal with metric signature (r, 1).
6. A Minkowski Spacetime with signature (2.999...., 1) such that the underlying smooth Euclidean space is 2.999... dimensioned.

Towards Formalization

Let's start torward the base cases. I'm probably very wrong here but it's worth attempting and fun. Maybe something useful can be gleaned from this thought experiment.

One way we might consider a novel way to obtain the above concept (within the realm of Euclidean-like spaces) is through the following process:

1. Given an R⁴ space: [R,R,R,R].
2. We observe that each element of the ordered set above is countable.
3. Perhaps we can apply standard techniques to construct the Reals from a finite or countably infinite sequence: Dedekind Cuts and/or Cauchy Sequences.
4. That process is likely straightforward.
5. Can we borrow insights from those well-known basic techniques to extend or populate a Cartesian Product with the missing/relevant values?

Super helpful article: https://plato.stanford.edu/entries/infinity/#InfiCoun

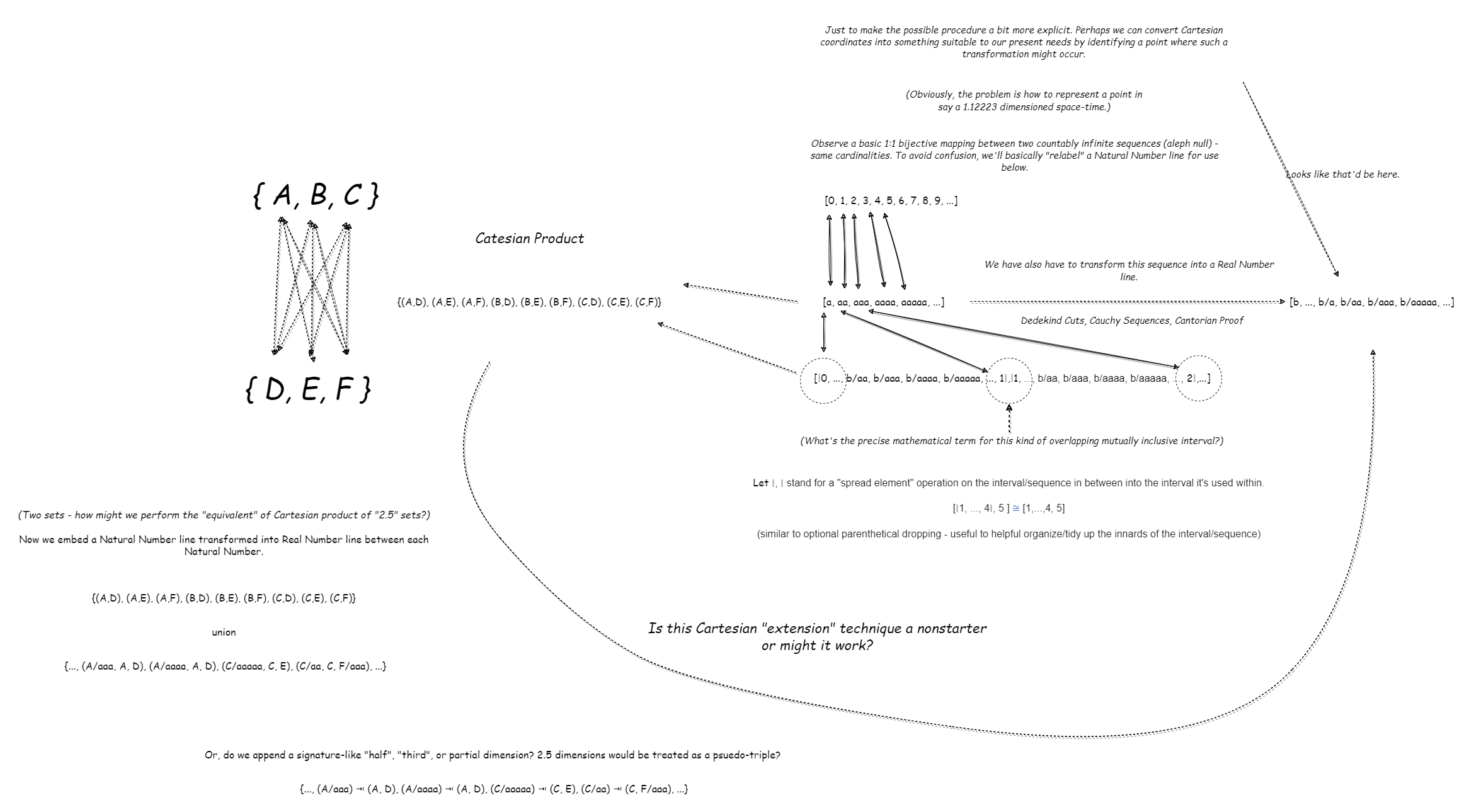
Let's use a simpler example to frame the problem and some possible approaches. So, {A,B,C} ✕ {D,E,F} = {(A,D), (A,E), (A,F), (B,D), (B,E), (B,F), (C,D), (C,E), (C,F)}. The difficulty arises in two related ways:

6. How does one represent 2.5 dimensions (at all)?
7. How does one represent the Cartesian Product (or whatever replacement/alternative) we might use? This entails representing something like a set with "2.5" elements.

Two possible lines of approach:

8. We "attach" a pseudo dimension to the otherwise standard Cartesian Product. Let ⭲ be just such an attachment: {(A/aaa) ⭲ (A, D), (A/aaaa) ⭲ (A, D), (C/aaaaa) ⭲ (C, E), (C/aa) ⭲ (C, F/aaa), ...}
9. We equip the standard Cartesian Product with another set (via Set-Theoretic union): {A,B,C} ✕ {D,E,F} ⋃ {..., (A/aaa, A, D), (A/aaaa, A, D), (C/aaaaa, C, E), (C/aa, C, F/aaa), ...} so that the resultant set isn't rectangular (elements can fail to have a uniform size or number of elements themselves).

Are these tractable approaches? Are they non-starters?

Partial Sets and Fuzzy Sets

So, a related problem. How does one represent a "partial set" of say 2.5 elements?

1. Fuzzy Sets? Fuzzy Sets have degrees of elemental inclusion/membership. So, perhaps A and B both have a degree of 1 whereas C has a degree of .5? That seems impure but might work as a starting point.
2. Otherwise, I think all Set-Theoretic concepts in use today use integered numbers/quantities of elements.

Apparently, some relevant topics have been explored in the landmark paper Fuzzy Topological Spaces by Cheng-Ming. Following the hunch above, perhaps:

3. (i) Since topological spaces are typically modeled as the product space of two or more sets and (ii) fuzzy sets might be used as model or to model partial dimensions (e.g. we might model 2.5 dimensions as A ∈ Ω, B ∈ Ω, and C ∈բ Ω where ∈բ maps C, Ω to [0,1]) perhaps it follows that Fuzzy Topological Spaces could be a model for partial dimensions above.
4. As far as I can tell, it looks like all Fuzzy Topological Spaces still invoke the use of integered-valued quantities of dimensions.
5. If so, tracking the Cartesian Product into Fuzzy Topological Spaces (within such a partial dimension model) might involve something like: {A, B, C} ✕ {D, E, F} = {(A,D), (A,E), (A,F), (B,D), (B,E), (B,F), (C,D), (C,E), (C,F)} where C and F are elements included via the fuzzy elemental inclusion operator ∈բ so that: (C,D) would say represent the Y coordinate D in the partial dimension C. (And, then would D have partial membership in the dimension of which C is a part of?)

Possibly, an interesting intersection of topics here. Looks like most (all) of the literature applies Fuzzy Topological Spaces and Fuzzy Sets to integered-valued topological spaces. I wonder if they could be models of the "partial dimensions" I'm describing above?

If so, are there alternative formulations?

Some Awesome Papers

1. https://www.mdpi.com/2227-7390/8/2/188
2. https://core.ac.uk/download/pdf/82238961.pdf
3. https://www.sciencedirect.com/science/article/pii/0022247X87900503
4. https://www.hindawi.com/journals/afs/2012/167939/