Sign, Identity, Relations
Thoughts about depictions of objects and relations. Allowing myself to be guided by some simple pictorial intuitions (that are often employed to do robust math) to see where it takes us.
How do we arrive at the intuition that circles and lines between them should be used to guide mathematical proof?
Definitions
- Object - a self-subsisting thing typically understood to be the referent of a proper name, a singular term, and individuated (for example, by Leibniz's Law).
i. An apple.
ii. Me.
iii. You.
iv. A photon.
v. The universe.
vi. Planet Earth.
vii. Single-celled organisms.
- Relation - something that obtains between one or more objects. A way that objects are situated with respect to one another.
i. Personal interrelationships.
ii. Mathematical relationships or operations like addition, division, subtraction, etc.
iii. Cardinal directions, location, and spatial coordinates.
iv. Your mug is resting on your table.
Depictions
Objects are standardly depicted as a completely contiguous closed circle:
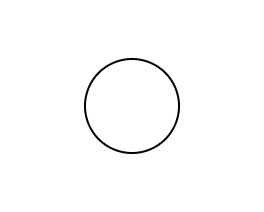
This aligns with our intuitive notions about objects:
- They have boundaries.
- They are (usually) spatial or at least located in some background space or universe.
- They self-subsist (do not flicker in and out of existence - they persist - one of the wonders about modern particles and Quantum Foam is that they defy this intuition).
- When overlapping, they retain their individual essence or identity (they neither merge nor blend, they are merely arranged in some kind of spatial arrangement, e.g.).
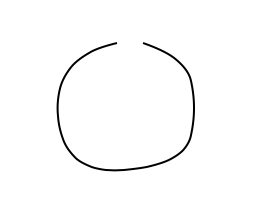
Here, we "cut" the circle producing a "U". Here, the individual object becomes something other than that.
Here, the intuition is that what was once an individual object has been transformed into something lacking a boundary, essence, and identity.
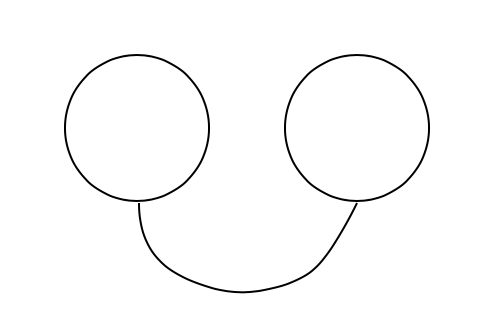
Now, we construct a simple-enough and standard depiction of a relation holding between two objects.
The key insight here is from the step above - that the relation is "really" a "cut" object!
The idea that objects are really a species of relation has been argued elsewhere. What if relations are a kind of object in disguise?
In Physics, the idea that particles (objects) had a dual nature (acting as both waves and particles) was a great discovery. I wonder if current ontology is still constrained by archaic notions that haven't begun to appreciate these kind of "dual nature" approaches to objectual (e.g. - of or pertaining to objects) approaches.
- Path Deformation
- On Connection Theory
- On Connection Theory #2
- Ontological Gaps
- Sign, Identity, Relations
- Sign, Identity, Relations #2
- Sign, Identity, Relations #3
- Fun Math Stuff and the Philosopher's Stone
- Fun Math Stuff and the Philosopher's Stone #2
- Fun Math Stuff and the Philosopher's Stone #3
- Relational Bundle Theory and Graphs
post: 4/24/2020