Remarks on Truth-Grounding and the Liar
This post summarizes several further thoughts and comments about a paper I wrote in graduate school.
Truth-Grounding and the Liar
The paper:
- Provided a philosophical solutionA solution that doesn't just describe how to solve a problem mathematically. It also explains why the problem emerged in the first place.: the root of the problem is the misapplication of the Truth-Predicate within alethic inferences (the set of sentences over which the T-Scheme ranges). That truth-reasoning can only be intelligibly applied to transparent truth-sentencesSentences whose alethic predicates may be eliminated without removing or altering the semantic content of the expression.. By restricting the T-Schema we achieve a classical solution to all alethic paradoxes, that's provably consistent, and whose only restriction falls upon sentences that cause alethic paradox.
- Provides a finite algorithm (the first) to classify finite sentences and determine whether they should fall into the extension (of the Truth-Grounded Predicate) or not. Provides an algorithm to address infinite constructions like Yablo's Paradox.
- Provides the first formal definition for alethic paradox (paradoxes stemming from Truth) - i.e. - the shortest proof resulting in contradiction that requires the use of T-Schema, F-Schema, etc.
- Does not cause further paradox. To wit, no presently touted solution fully eliminates all alethic paradox since in "solving" the initial problem, they cause Revenge.
- Respects the meta-linguistic property called reflection (in computer science) or predicativity (in formal logic). Sentences can be self-referring or self-reflexive. No solution that disallows these (simpliciter or otherwise) is acceptable.
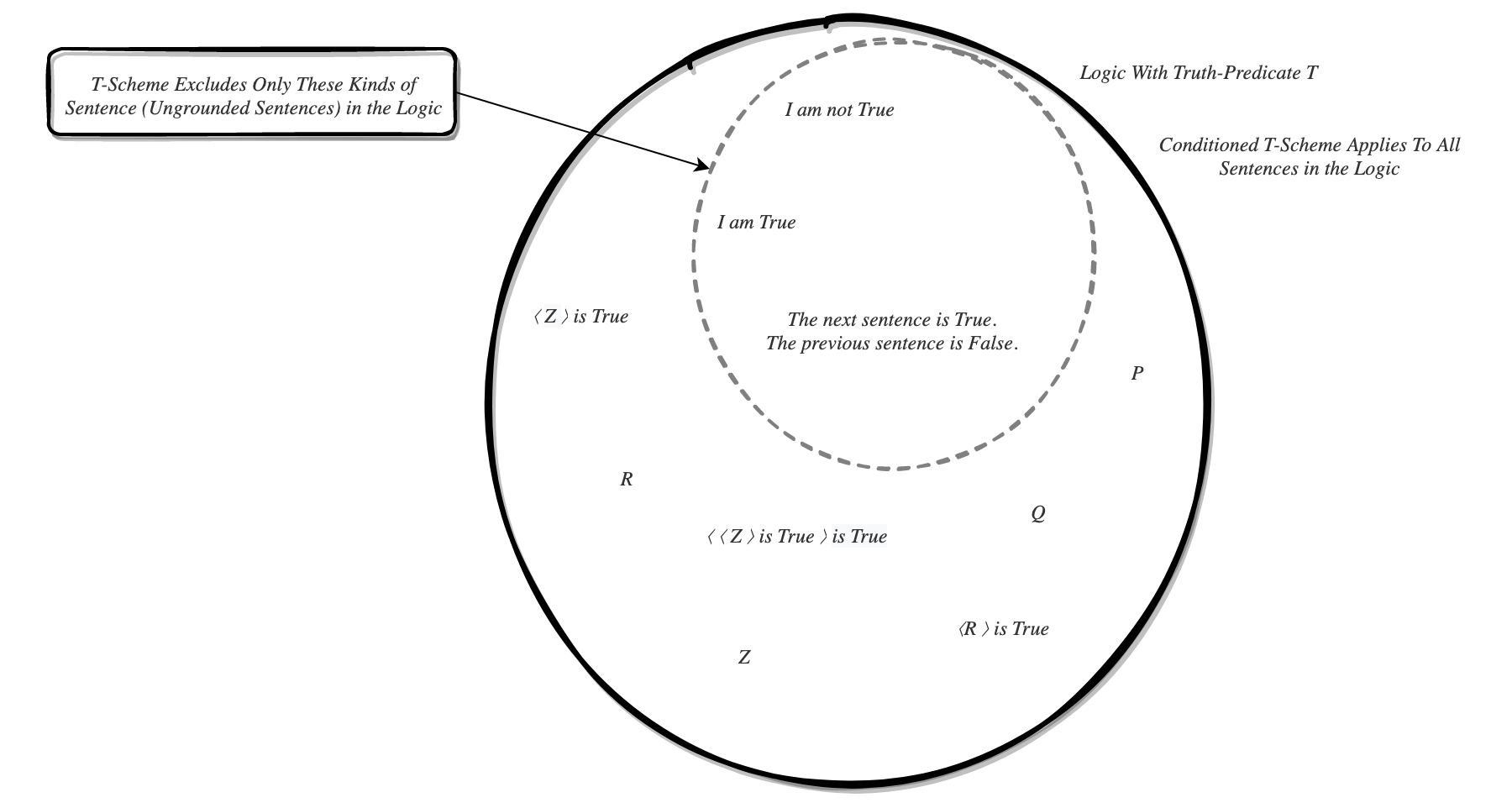
- Per (2), creates a set of grounded (here, "acceptable" ... a nod to Kripke's Fixed Point work) sentences that meet all philosophical and mathematical criteria. Namely, transparency/truth-eliminability, can be self-referring, is semantically closed, does not cause further paradox, etc.
- Can be applied to any other alethic paradoxes including Curry's Paradox (the same Curry that the concept of Currying in functional programming comes from), Liar Cycles, and Yablo's Paradox.
- Respects Truth-Teller sentences by allowing them to be syntactically valid, semantically meaningful, but banned from Alethic reasoning.
- Does not reject bivalence and preserves classical logic.
- Is the only formal solution that respects (here, is "consistent with") the empirical observation that people have offered four prima facie compelling kinds of solutions to the Liar Paradox in the first place (that the Liar Sentence is True, that it is False, that it is Neither True Nor False, and that it is Both True and False) that have framed the entire historical debate since Antiquity.
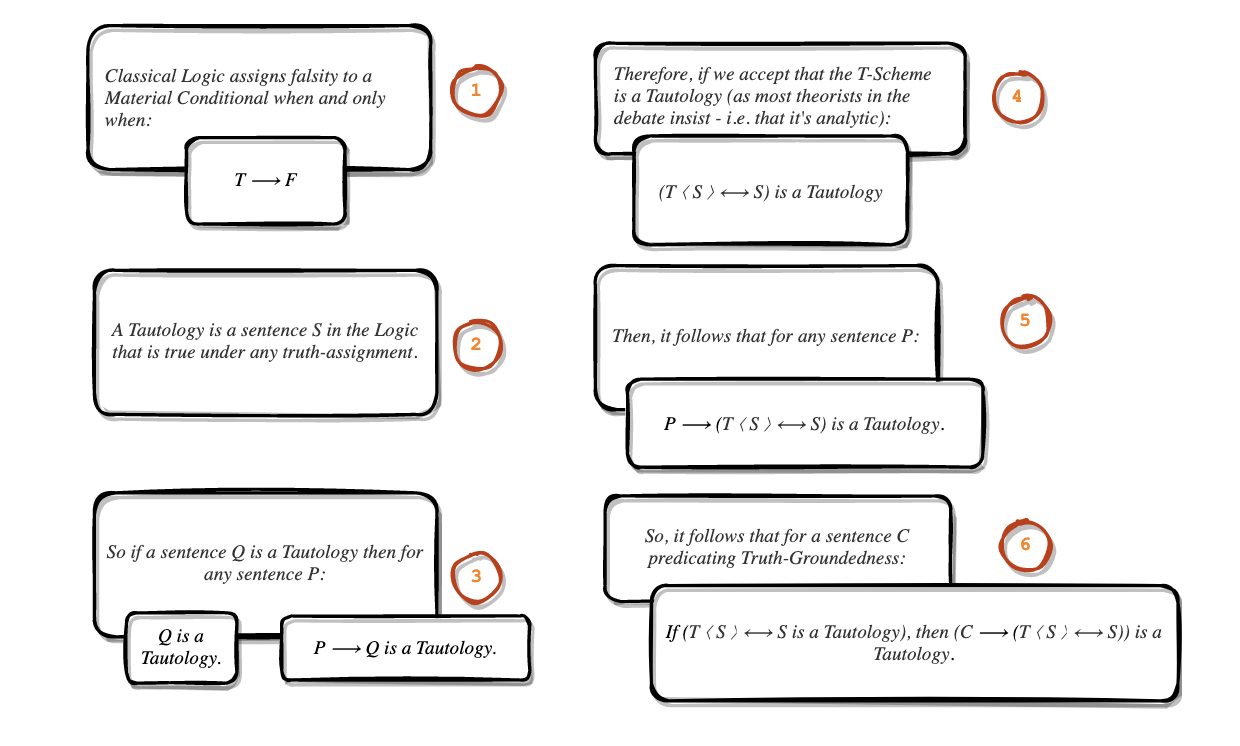
No other solution incorporates that empirical fact within the theory - they merely dismiss other views as errant, misguided, ignorant, or wrong. Here, such approaches are fully consistent with the view (and as noted below, if they assert that T-Scheme is analytic, they also entail the Truth-Grounding approach - if P is a tautology so is Q implies P for any Q).
- Is the only formal solution that respects (here, is "consistent with") the empirical observation that most people think the Liar Sentence is semantically valid though they never try to reason with it.
Additional Desiderata
However, I think the following should be added to, supplement, or stand out from the original desiderataDesirable standards of evaluation that are often collectively determined - how one is to judge a problem and determine its success or failure.:
- T-Scheme should be analytic (conditioned or not).
- The solution should be the most parsimonious relative to its alternatives.
i. The solution should involve as few additional theoretical assumptions as possible to successfully address the problem.
ii. Additional assumptions about reference, context, language, semantics, and so on are calculated as costs since the truth of the solution is also contingent on the truth of these other theories.
- The solution should identify the root of the problem not just for the liar paradox but for all alethic paradox.
- The solution should cohere maximally with other theories. It should be as theory-agnostic as possible in line with 2.
- The solution should provide an effective procedure or algorithm to mathematically define the class of problematic expressions. We note that the meta liar ('the liar sentence is true' is true) also runs afoul of alethic paradox.
- The solution should apply equally well to semantically closed and unclosed languages.
- The solution should solve all alethic paradoxes, including Yablo and Revenge.
Here, only Truth-Grounding and the Liar meets all of these conditions.
A Few More Arguments
- Classical instability. Is classical instability (For a wff p and interpretation function I: I(p) = T and I(T(p)) = ~T) really a strike against the theory? Doesn't classical instability occur in any Classical solution?
i. Doesn't it provide mathematical and structural support for the empirical observation that people have diverging views about the liar paradox?
ii. Wouldn't a true theory capture that empirical observation? No other theory set does that.
iii. And no small wonder since we're all using classical logic in our metalogic used in these debates.
- Analytic - if T-Scheme is indeed analytic (which everyone but most restrictionists believes) then so is the restricted T-Scheme.
- Note that the added consistency proof and truth-in-all-models prove the analyticity of the restricted T-Scheme as well.
- The restricted T-Scheme debate shifts inquiry to the proper area of focus, which sentences does the T-Scheme apply to? (A non-restrictionist says all.)
Truth-grounding, here, involves a privileged set of sentences from which derived true sentences can come. In sentential logic, propositions compose sentences (containing the logical connectives).
If (T-Scheme) exists in a language L then so does: (P → T-Scheme). Thus, this solution piggy-backs any other theory. The moment a condition C is added to a language so this, Truth-Grounding theory emerges in it.
Traditionally, "Universal Laws" or other axiom systems so-proclaimed have gradually seen their tenability recede in the face of greater experimental evidence or advancements in mathematics (Euclidean Geometry v. Hyperbolic Geometry, Set Theory v. Category Theory, Netwon's Laws v. Quantum Theory, etc.). Why should we think our theory of truth should behave otherwise? In other words, previously assumed universal rules end up being mere ceteris parabis conditions (conditions that hold given some specific set of circumstances). And that's exactly what the restrictionist approach is!
Additionally, logic gates are commonly used throughout computer science. Reversible logic gates used the notion of a check (controlled logic gate). These are primitive (fundamental, most basic) notions at the hardware level of computer design. Here, the restrictionist approach aligns with the contemporary computer science and electric engineering!
Clarifying
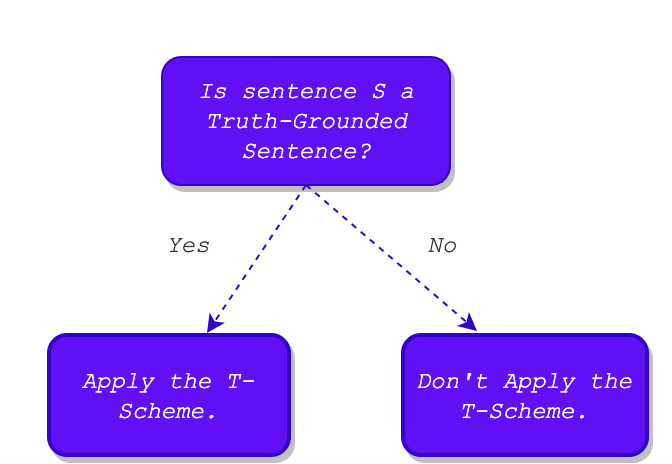
i. A grounded sentence S for a language L is a sentence with a specified property P to serve as the foundation or starting point for a procedure, operation, or use.
ii. Truth-grounding is formally defined as specifying a set of sentences (not necessarily wff) satisfactory for our theory of truth.
iii. A algorithm to define the set of truth-grounded sentences is defined. Call this TGA.
Note: TGA is finite since every sentence in L is finite (though it can be extended to apply to infinite sequences).
By 'Unqualified T-Scheme' I mean 'unconditioned T-Scheme' (without or lacking caveats).
A Second Classical Solution?
What about mathematical diagonalizationA technique pioneered by Cantor to prove several famous results in Number Theory.? To which sentences does this method apply? What are the appropriate constraints (if any)?
Presently, by (totally) unrestricted diagonalization over definitions (letting the name of sentence stand on the right-hand side and allowing names within or as wff along with the somewhat sloppy and often assumed equivalence between df= and ≅), we (obviously) find:
- S df= ~S
- S df= Q
- S df= R
- R df= ~S
- and so on.
This is problematic. Perhaps the problems lie less with Classical Logic, T-Scheme, or our meta-logical concepts (i.e. - Tarski's metalogic, object logic/metalanguage, object language concepts) but rather with the constraints on assignment and use of name-forming operators and sentences.
That's great since there's little discussion on that in the literature (i.e. - typically, there's a hand-wavy "an adequate name-forming operator" mentioned) and an opportunity to clarify our logical concepts. This may also help to refine the concept of formal definitions in the first place.
i. Thus, we may combine the TGA with improved constraints on the selected name-forming operator to potentially provide a cleaner classical solution.
ii. This is not only of significant mathematical interest but of great philosophical interest as well (naming baptisms, Kripke's On Naming and Necessity, etc.).
Special thanks to Richard Han for some early insights into the concept of mathematical definitions. I've expressed my gratitude for his insights elsewhere but wanted to add those comments here as well!
Some Extra Thoughts
- I recommend the positive view now. That [my solution] (the combination of Solomon Feferman's brilliant axiomatic insights and JC Beall's truth-transparency criteria with a tincture of original algorithm design) represents the best solution in classical logic. Along with an under-girding theory of truth.
- I'm also a logical pluralist in the sense that there are, strictly-speaking, numerous truth-predicates. Each predicate is formally understood through the rules of inference and wider logic in which it is embedded. We are thus able to compare and classify truth-predicates, scientifically.
- The truth-predicate as presented here is the most-classical truth-predicate (henceforth MC-TP). Substructural truth-predicates preserve T-Scheme but lose some of the classical logic (they reject certain rules). In both cases, there are well-defined boundaries that where either all of the classical logic ranges or all of the T-Scheme ranges but not both.
- David Ripley's super rad and helped me out by raising objections and being ultra-supportive (in philosophy that's a compliment - it means that someone thinks there's something worthwhile that needs some work rather than something irrelevant or silly) and chatting about this shared area of interest back in grad school.
- So too were Solomon Feferman, JC Beall, Graham Priest, and Valia Allori.
Regarding KF 1983, 1991
From: plato.stanford.edu - truth-axiomatic (Section 4.4 Axiom 1):
∀A(AtomSentPA(A)→(TA↔Tr0(A)))
And a little lower:
"KF itself is formulated in classical logic, but it describes a non-classical notion of truth. For instance, one can prove
T[L]↔T[¬L]if L is the Liar sentence. "
A few comments with respect to the above:
- In hindsight, I should have used a slightly more clear nomenclature for axiom schemata/form:
[Kripke-Feferman] C(S) → (Tf(S) ↔ S)to better distinguish from the original system above. Perhaps using[Kripke-Feferman*]. While not a point of confusion among academics, this might have invited some confusion out of academia. - One will note that my articulation is an abstraction of the first.
- The motivation for Truth-Basing (as I now call it) or Truth Grounding is given by the antecedent in the original formulation. For example, any formulation of Classical Logic defines wff's recursively from basic Atomic Propositions (then proceeds to define compelx wff's). Ditto for Truth-Assignments (we begin with Atomic Propositions, then map Sentences). So, I allow the Truth-Predicate to be built in the same way. (I originally took the antecedent condition in my paper to be inspired by the original Nobel Prize winning-equivalent forumation above.)
- Also, since I simplify the axioms by pulling the antecedent condition out (along with providing the finitely decidable algorithm above) in a slightly more nuanced way, this vastly simplifies the result and allows Consistency Proof to be inductively shown (at the end although I don't call it that by name).
- As a result, the improved formulation I offer that builds off the incredible work of Kripke, Feferman, Beall, and Ripley in the original ways I've described above and elsewhere is consistency (their consistent models of the Liar since the Truth-Predicate is separated from the Truth-Assignment).
- Some of the above is explained (indirectly) in the paper or elsewhere already but I feel it important to further clarify that here.
- Remarks on Truth-Grounding and the Liar
- Remarks on Truth-Grounding and the Liar #2
- Ground Facts and Truth
- Ground Facts and Truth #2
- Addressing Metalogical Justification
- Propositional Stability and Cohen Forcing
- Truth as a Prosentential Operator
- The Liar Paradox in Programming
- Fun Math Stuff and the Philosopher's Stone
- Fun Math Stuff and the Philosopher's Stone #2
- Fun Math Stuff and the Philosopher's Stone #3
- Restrictionism and the Four Corners of Logic
post: 3/18/2018
update: 10/20/2018
update: 12/30/2018
update: 4/2/2020
update: 6/7/2020
update: 6/12/2021
update: 6/13/2021
update: 7/17/2022
update: 12/3/2023