Metaphors, Math, and Semantics
Wittgenstein famously threw away the ladderHe acknowledged the metaphysical contradictions with representationalism. On the one hand, we need representationalism, on the other hand it's untenable. due to difficulties with the traditional conception of language's relationship to the world (via transcendental and, on his view, contradictory metaphysical relationships).
What about Posthuman languages that are not restricted in the same manner as human languages (assuming his critique of language was correct - he came back later and argued that meaning in language derives from language games and their attendant forms of life usually enshrined in meaning as use theories)? Where Wittgenstein saw a ladder to be disposed of, perhaps there's a skyhook?
The metaphors that are at play in depicting these simple relationships (though riddled with metaphysical worries as they might be) give rise to powerful mathematical structures. Might we borrow heavily from well-established maths to define these metaphors more fully? In doing so, the simple arrows or other symbolic representation systems at use in such discussions might give way to powerful new ways of thinking about things - ways that are indeed quite counter-intuitive to the arm-chair philosopher not acquainted with them. Pointing relations (how reference and correspondance are usually thought of)? But these mappings can be conceived even if we give a metaphysical gloss (reminded here of Carnap's distinctions between different uses of the word "exists") that cannot be sustained under scrutiny.
Pictorial Metaphors
In philosophy, it's common to see the following kinds of metaphors or pictures:
i. Pyramidal layers.
ii. Arrows and Pointing.
iii. Referential pointers.
iv. Webs of belief and inference.
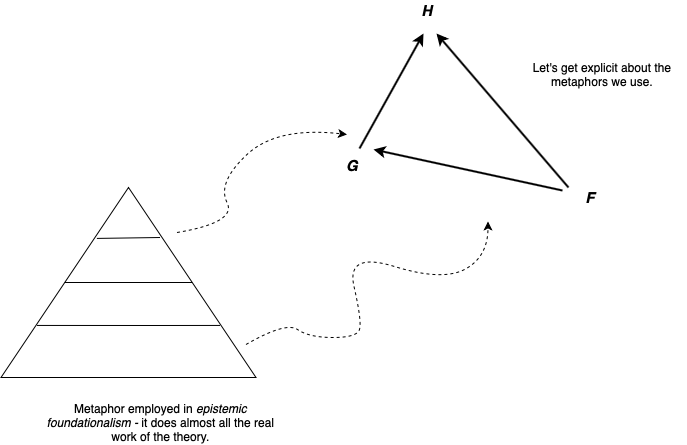
These are often confused and implicit.
These should properly employ geometric, topological, mereological concepts and techniques along with other systems to understand and explain them.
And, when this has been demonstrated and done, will the mysteries disappear? Will we be left with robust systems all the way through?
Noting that "pictures" (e.g. metaphors) do most of the work at the bottom of many philosophy theories has had its share of early observers - watch: Putnam.
"Pictures" are inherently spatial - inherently geometric. Read: SCO and connection Theory.
I am reminded of the sign outside the original Platonic Academy (from which the word "academic" derives): "Let no man enter here who is ignorant of geometry".
- Inner Semantics
- Inner Semantics #2
- Inner Semantics #3
- Inner Semantics #4
- Metaphors, Math, and Semantics
- Posthuman Languages
- Posthumanism and Transhumanism
- Symbol Binding
post: 1/26/2019
update: 1/22/2020
update: 3/10/2020