Gerard’s Totally Obvious Corollary
I got into thinking about Sophons and Trisolarans after reading the great Wired mag article and NYT review. In that story, an ant-sized species creates a supercomputer by unfolding a proton. Protons are miniscule but when unfolded, the available surface area is equivalent to the Earth's surface. A very powerful supercomputer indeed.
While the conceit's cool (the conceit being that 11-Dimensional String Theory is true), it's probably false. It did however remind me about two topics:
- The Banach-Tarski Paradox I encountered while dealing with another of Tarski's solutions (to the Liar Paradox).
- Holographic Shadowing
Note: I shall refer to the Banach-Tarski Paradox as BTP henceforth.
Non-transfinite
A sphere with infinite points on its surface can be cut five ways and reassembled so as to have two identical spheres (identical to the original).
This is partly due to the nature of classical infinite cardinalities (like ℵ₀). In the original scenario explored by BTP, the surface is ℝ (ℵ₁).
Note: Below I shall write |A| to denote the cardinality of some set A.
Fact 1. Infinite but not transfinite sequences can be mapped into some infinite sequence.
Proof. Obvious. ℕ is a subset of ℝ.
Intuitively, this should guide us. |ℕ| < |ℝ| → |2ℕ| < |ℝ| since |ℕ| = |2ℕ| (e.g. - in terms of cardinality).
Therefore, if A is an infinite subset of ℕ and ℕ ⊂ ℝ then A can be duplicated (e.g. - can be found on the surface of the resultant two copies of the original sphere) using the means above.
So, provided that there’s a mapping from infinite but not transfinite set A to |ℕ| and that the appropriate cutting and reassembly procedure is used, A can be duplicated in |ℕ|.
Finite
Can this be done? I think so.
- Every finite and transfinite sequence (or set) A has at least one finite subsequence. If then, some sequence (or set) A is duplicated so too is that finite subsequence.
- Second, each element of ℝ can be assigned a unique index. And, that index has finite subsequences. Provided that each point has an index and that these are duplicated, so too does it follow that the finite subsequences are as well.
In these cases, the finite sets piggyback the infinite ones getting duplicated along the way.
Three-Sphere
Mapping to a 3-Sphere (extending BTP to 3-sphere).
Does this apply to a 3-Sphere and not just spheres?
Dimensional unpacking / packing
Some mathematically trivial cases.
Unpacking (to Lower Dimensions):
- A solid 3D object unfolded into 2D space. The unfolded area will be equivalent to the volume.
- An "empty" 3D object (surface area only) unfolded into 2D space. It’s equivalent in unfolded area to the surface area.
- A 3-Object - filled with overlapping (potentially solid) objects - can have a much greater unfolded area than the volume. As much as N where N × volume is the total number of solid but overlaid 3-Objects.
- When we unpack ℕ³ to ℕ², we arrive at a broken symmetry. One dimension has no proportion and the others have the remaining area.
- So, unpacking the Nth dimension into N-1th dimension results in the N-1th dimension having proportionally more of the area or volume of the object.
We might express this more formally. Take a cube in ℕ³. The total ratio of the cube’s volume and/or surface area is distributed equally across each of the 3 dimensions.
As we unpack (into lower dimensions) we break the symmetry - moving the total surface area or volume into a hyperplane.
Unpacking (to Higher Dimensions):
- What about the other way? What about unpacking from N to N+1?
- By moving one dimension higher we have gained an extra rotational vantage point, another degree of freedom. This can assist us with inspecting objects.
Unpacking (in reverse) makes the current N-dimensional object a hyperplane in N+1 dimensions.
Stretching:
- Stretching is just to take N to another dimension (a line of length N becomes a square N×N, then becomes a cube N×N×N in 3D).
- We observe that the ratio gained (N, N:N, N:N:N) is strictly proportional in all dimensions the object is stretched by.
Holographic Principle:
- The Holographic Principle (succinctly expressed for simple geometric scenarios) - we can represent N dimensions in N-1.
Holographic Shadowing:
In all the scenarios above, objects gain no extra volume or space unless an explicit operation is being performed (e.g. - stretching).
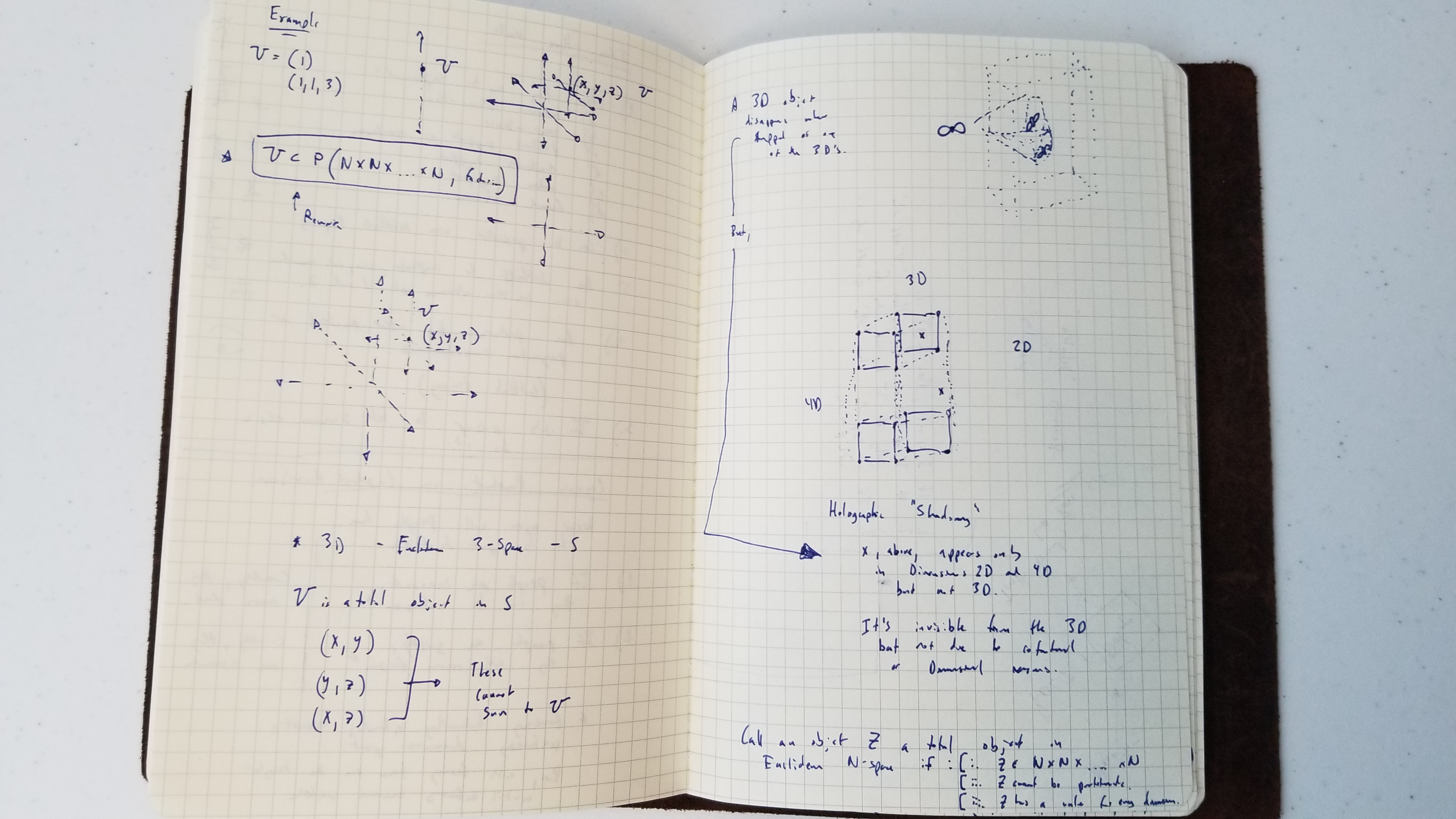
Previously, in 2018, I outlined a brief sketch of an idea I called Holographic Shadowing and briefly alluded to it here.
Let's dive into this more!
- An object exhibiting Holographic Shadowing by definition violates the mathematical properties seen above.
- Objects of this nature can maintain the symmetry of proportionality as one moves between dimensions.
- In the Nth dimension the object could have volume V but have V×V×V in the N-1 dimension after unpacking.
- Only an object with Holographic Shadowing can, by virtue of its nature alone, suddenly appear with more area/volume as it is inspected in higher or lower dimensions.
- An object with Holographic Shadowing does not change in area or volume as one moves between dimensions. Rather its nature varies by dimension (is defined or characterized by varying areas or volumes) and is fixed (unless an explicit operation or transformation is performed on it).
I think this is more akin to BTP (in spirit) because the specific operation that's performed allows one to disassemble and reassemble an infinitely pointed area into two or more equal copies.
An object exhibiting Holographic Shadowing can suddenly duplicate it's volume by moving to the appropriate dimension.
Why does this matter?
What if we could copy finite physical objects in the manner above?
i. It’s an alternative kind of manufacturing that wouldn’t require factory-like input-outputs.
ii. Just five transformations of an infinitely-pointed surface.
Plus, such surfaces might be useful for hyper-computation which allows for ℵ₀ operations in finite time.
With such a system, I could, theoretically, count all the numbers before dinner and duplicate my favorite car an infinite number of times over before desert!
Fun Resources
- Dimensions and Unpacking
- One-Way Functions
- General Method #2
- ZQL
- Path Deformation
- On Connection Theory
- Half Dimensions
- Fun Math Stuff and the Philosopher's Stone
- To the Infinite from the Finite
- On Proofs and Diagrams in Math
post: 6/25/2020
update: 7/8/2020